Neuroscience, neural nets, and nonequilibrium stat mech

DeWeeseLab    DeWeeseLab   

About the lab

We are the lab of Michael DeWeese at UC Berkeley. Our interests fall into three rough categories:

Nonequilibrium statistical physics.
Understanding and designing biomolecules and molecular-scale machines will ultimately require deeply understanding statistical physics far from equilibrium. To that end, we're working on developing work-energy theorems for active matter systems and optimal control protocols for systems driven out of equilibrium. We often use techniques from control theory and Riemannian geometry.
Machine learning theory.
Deep neural networks have enabled technological wonders from machine translation to image generation, but, remarkably, nobody has a principled understanding of how they work and what they can do. To fill this gap, we're working on developing first-principles theoretical understanding of neural networks, often finding use for tools and concepts from statistical physics. We're also interested in kernel methods and sampling algorithms.
Systems neuroscience.
Despite the wealth of neural data acquired in recent years, scientific understanding of how the brain works remains rudimentary. To make progress towards this, we develop biologically-plausible algorithms to model sensory processing and other forms of neural computation, often relying on coding principles such as maximizing sparseness or information flow. Our models clarify the computational roles of different neural populations and provide specific, falsifiable experimental predictions about the structure and activity patterns in biological neural networks.

Selected recent work

See here for a complete list.

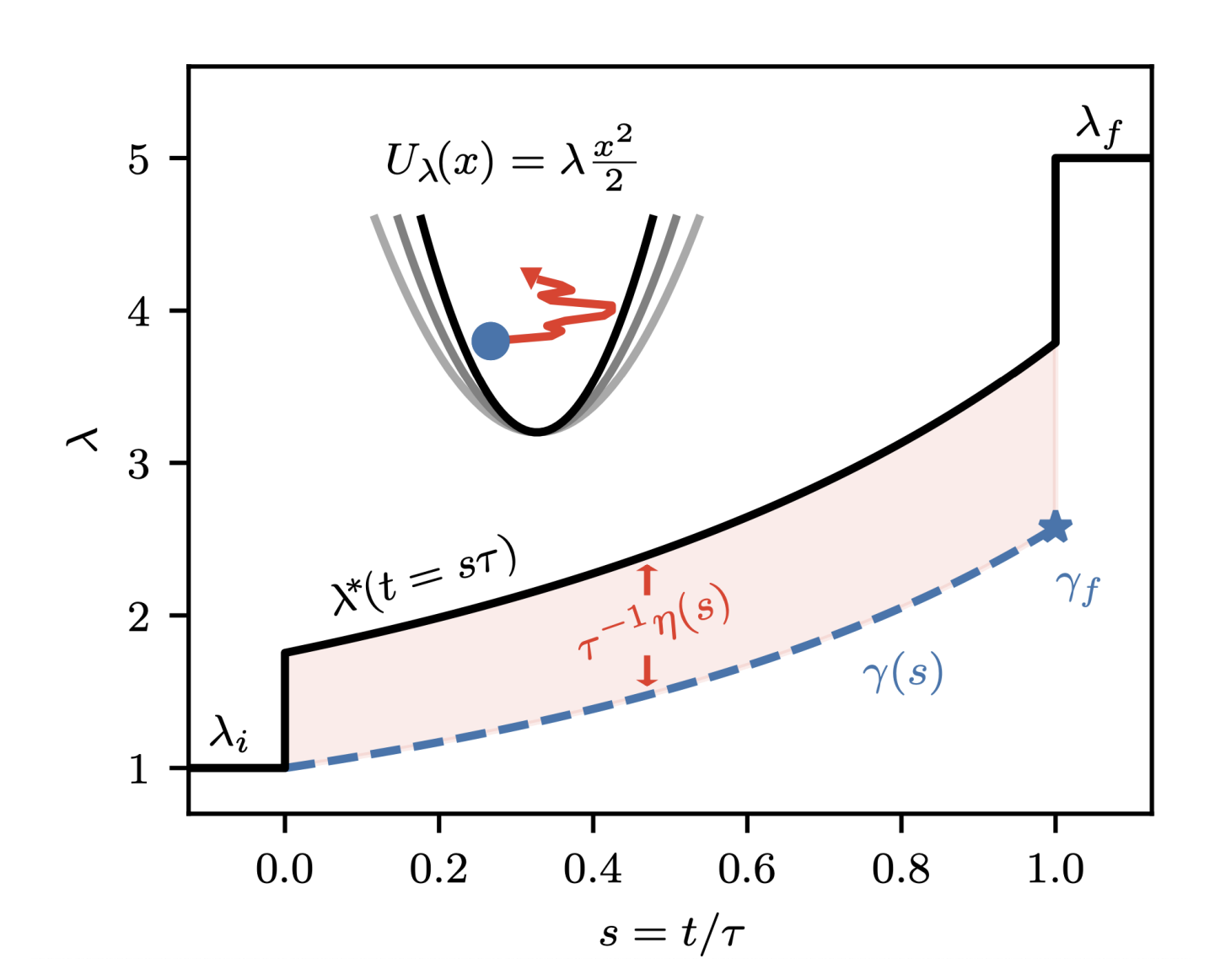
Equivalence between thermodynamic geometry and optimal transport

Thermodynamic geometry geodesics are optimal transport solutions

For a controllable thermodynamic system, what is the work-minimizing protocol transitioning between two states? It is known that if the transition is allowed to be slow, then the optimal protocol is a geodesic of the "thermodynamic geometry" induced by the Riemannian friction tensor defined on control parameters. We demonstrate that thermodynamic geometry--previously thought of as an approximate, linear response framework--is actually equivalent to optimal transport. From this equivalence, we show that optimal protocols beyond the slow-driving regime may be obtained by including an additional counterdiabatic term, which can be computed from the Fisher information geometry. Not only are geodesic-counterdiabatic optimal protocols computationally tractable to construct, but they also explain the intriguing discontinuities and non-monotonicity that have been observed before in optimal, work-minimizing protocols.

[arXiv]

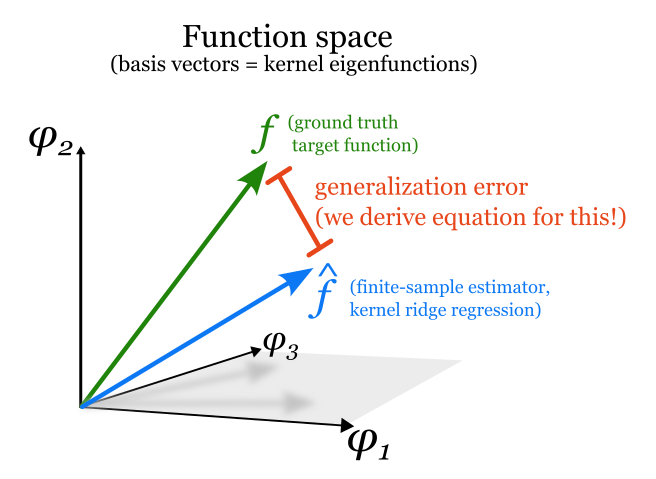
The Eigenlearning Framework

The eigensystem of a kernel predicts its generalization capabilities

The ability of neural networks to generalize without overfitting, despite having far more fittable parameters than training data, remains an open question. In this paper we derive equations that fully explain the generalization ability of a certain kind of neural network: very wide networks with suitably small learning rates. When trained, such networks are equivalent to kernel ridge regression. Our equations derive from the kernel's eigenvalues and the eigencoefficients of the target function; together, this eigenstructure captures all the salient properties of the network architecture, the data distribution, and the target function. In particular, the central object in our equations is a scalar we call learnability, which accounts for the kernel eigenstructure, the quantity of training data, and the ridge regularization strength. We find that the learnability of a target function is tractable to estimate, and our framework provides a theoretical explanation for the "deep bootstrap" phenomenon described by Nakkiran et al (2020), representing a major advance in understanding generalization in overparameterized neural networks.

TMLR '23 [arXiv] [code]

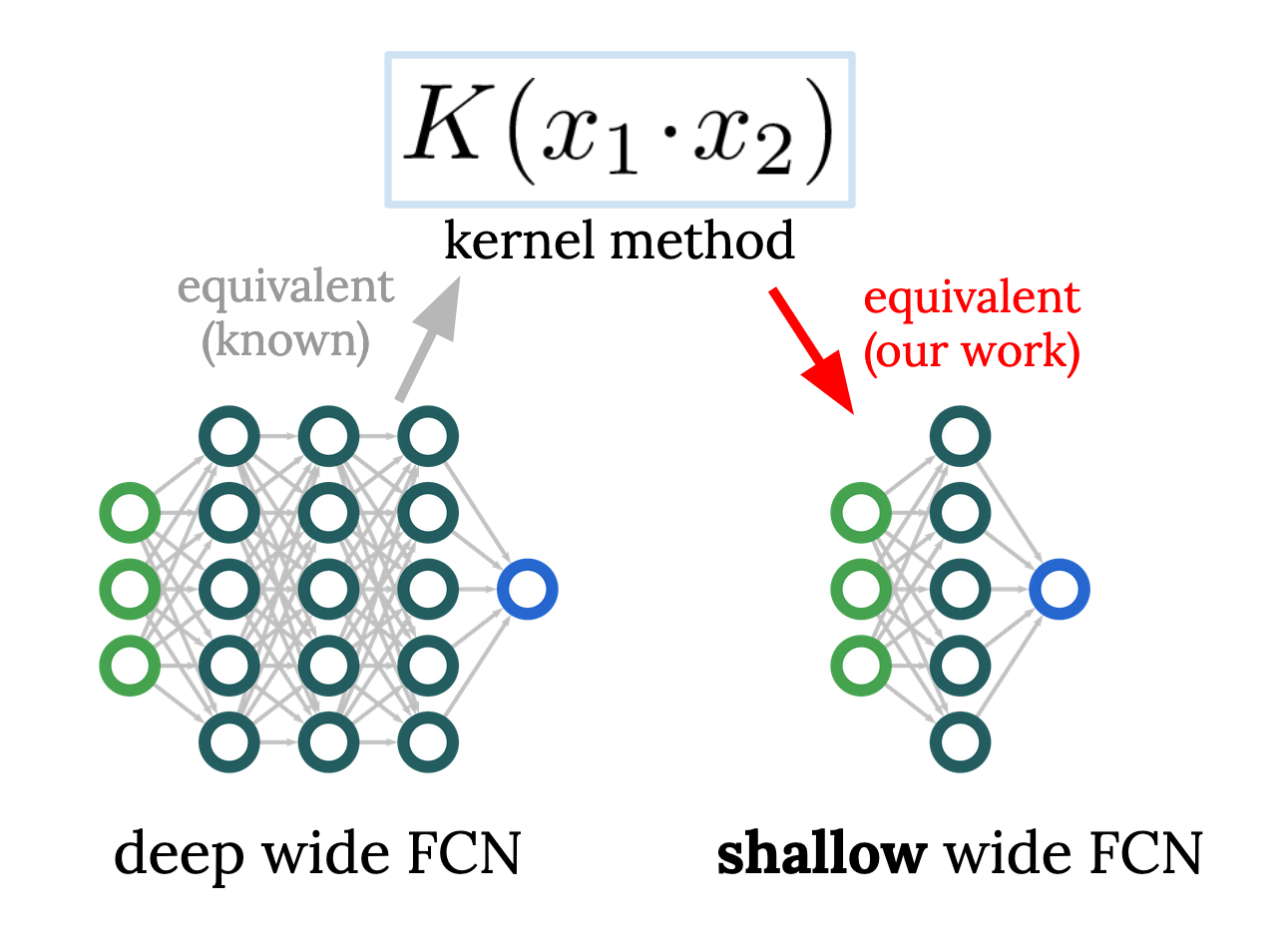
Reverse engineering the neural tangent kernel

A first-principles method for the design of fully-connected architectures

Much of our understanding of artificial neural networks stems from the fact that, in the infinite-width limit, they turn out to be equivalent to a class of simple models called kernel regression. Given a wide network architecture, it's well-known how to find the equivalent kernel method, allowing us to study popular models in the infinite-width limit. We invert this mapping for fully-connected nets (FCNs), allowing one to start from a desired rotation-invariant kernel and design a network (i.e. choose an activation function) to achieve it. Remarkably, achieving any such kernel requires only one hidden layer, raising questions about conventional wisdom on the benefits of depth. This allows surprising experiments, like designing a 1HL FCN that trains and generalizes like a deep ReLU FCN. This ability to design nets with desired kernels is a step towards deriving good net architectures from first principles, a longtime dream of the field of machine learning.

ICML '22 [arXiv] [code] [blog]

Redwood Center and Physics at UC Berkeley